- Autore Matthew Elmers elmers@military-review.com.
- Public 2023-12-16 22:17.
- Ultima modifica 2025-01-24 09:27.

In questo articolo, proveremo a determinare la durata dell'armatura russa della prima guerra mondiale. Questa domanda è estremamente difficile, perché è estremamente scarsamente trattata in letteratura. E il punto è questo.
È noto che alla fine del XIX secolo, le principali potenze marittime nella costruzione di navi da guerra passarono alle armature realizzate con il metodo Krupp. Ma questo non significa affatto che da allora l'armatura delle navi di tutti questi paesi sia diventata equivalente.
Il fatto è che la "ricetta classica" per l'armatura di Krupp (nota anche come "qualità 420", creata nel 1894) non è rimasta invariata, ma è migliorata. Almeno da paesi come Inghilterra e Germania. Ma come esattamente si è perfezionato e a quali risultati sono arrivati i maestri dell'armatura di vari poteri - questo, purtroppo, non lo so per certo.
Prova del fuoco
La resistenza ai proiettili dell'armatura russa può essere determinata con una precisione accettabile, grazie al bombardamento sperimentale della vecchia corazzata "Chesma", riclassificata come "nave esclusa n. 4". Sulla nave è stato creato un compartimento sperimentale, copiando la protezione di varie parti delle corazzate di classe Sebastopoli, e per la purezza dell'esperimento è stato anche dotato di molti dispositivi che tali parti dovrebbero avere. Così, ad esempio, nelle casematte furono installati tubi del vapore (che passavano lì su corazzate), fucili a pompa, dispositivi di controllo del fuoco e cavi elettrici, ecc.

Quindi il compartimento sperimentale è stato sparato con varie munizioni di calibro da 6 a 12 pollici, inclusi, ovviamente, gli ultimi proiettili perforanti e ad alto potenziale esplosivo da 305 mm. Detto questo, i rapporti di prova sono molto completi, come dovrebbe essere in questi casi. Contengono non solo una descrizione delle conseguenze di un colpo, ma anche la velocità del proiettile nel momento in cui colpisce l'armatura, nonché l'angolo con cui il proiettile e l'armatura si incontrano.
Tutto ciò ci consente di calcolare la resistenza dell'armatura russa in relazione agli ultimi proiettili domestici da 470, 9 kg, secondo la stessa formula di Jacob de Marr, che ho più volte citato in precedenza. Ma lo citerò di nuovo, in modo che il caro lettore non debba sfogliare gli articoli precedenti. Il rapporto tra la qualità del proiettile e la durata dell'armatura in questa formula è descritto dal coefficiente "K". Inoltre, maggiore è questo coefficiente, più forte è l'armatura.

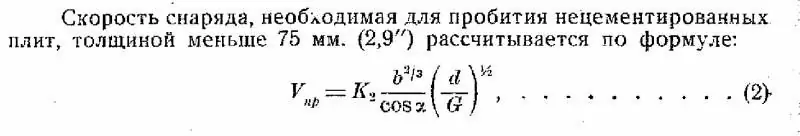
Una certa difficoltà nella valutazione dell'armatura russa è creata dal fatto che i proiettili sono stati testati principalmente e non la resistenza finale dell'armatura della protezione delle ultime corazzate. Sembra essere - qual è la differenza? Ma in effetti è molto significativo. Quando vengono testati i proiettili, l'interesse è nella loro distruzione affidabile dell'armatura alle principali distanze di battaglia. Quando l'armatura viene testata, c'è interesse per le condizioni ultime in cui può ancora proteggere la nave.
Tuttavia, le statistiche degli hit sulla "nave esclusa n. 4" consentono ancora di trarre alcune conclusioni.
A proposito di sparare a un'armatura da 250 mm
Sfortunatamente, i colpi in armature da 125 mm o meno non ci interessano - in tutti i casi si è scoperto che o l'energia del proiettile era più che sufficiente per penetrarlo, o gli angoli di impatto erano così piccoli da dare un rimbalzare. In altre parole, per determinare la durata dell'armatura, le statistiche dei colpi su armature di 125 mm e inferiori sono inutili.
Una questione diversa sta colpendo la spessa armatura da 225 mm e 250 mm, che daremo un'occhiata più da vicino.
Cominciamo con 250 mm di armatura, che proteggevano le pareti della torre di comando della "nave esclusa n. 4". In totale, sono stati sparati 13 colpi a questa timoneria, ma alcuni di essi sono stati sparati sul tetto e altri da proiettili ad alto potenziale. I proiettili perforanti sono stati sparati contro un'armatura da 250 mm solo 5 volte.
Il colpo più potente è stato il n. 6 (numerato secondo i rapporti di prova). Un proiettile perforante da 305 mm ha colpito la piastra dell'armatura con un angolo di 80 ° (10 ° dalla normale) a una velocità di 557 m / s. Un proiettile avrebbe una velocità simile di 470,9 kg a una distanza di soli 45 cavi. È vero, l'angolo di deviazione dalla normale sarebbe inferiore a - 6, 18 °.
Naturalmente, il proiettile ha perforato l'armatura. Per reggerlo sarebbe necessaria un'armatura con una "K" superiore a 2.700. E questo è un valore esorbitante, anche per gli standard dell'armatura molto più avanzata della seconda guerra mondiale. I calcoli da me effettuati mostrano che a distanza il cannone russo 305-mm / 52 mod. 1907 potrebbe penetrare la corazza di Krupp da 433 mm "qualità 420".
I restanti 4 colpi sono stati sparati in condizioni uguali. La velocità del proiettile sull'armatura era di 457 m/s, gli angoli di incontro con l'ostacolo erano di circa 80° (deviazione dai normali 10°). Secondo i miei calcoli, i proiettili russi avrebbero una tale velocità a una distanza di 75 cavi, ma l'angolo di incontro con un ostacolo sarebbe peggiore - 76, 1 ° (deviazione dal normale - 13, 89 °). In tali condizioni, secondo i calcoli di cui sopra, sono penetrati 285,7 mm di corazza Krupp (con K = 2000). Ma in realtà, tutto si è rivelato non così inequivocabile.
Durante lo scatto n. 11, tutto è andato liscio. Il perforante superò la corazza da 250 mm, colpì la parete opposta della timoneria e già allora esplose, creando una buca nel punto di impatto profonda 100 mm. Quando ha sparato n. 10, anche l'armatura era rotta. Ma non è del tutto chiaro quando si è verificato esattamente lo scoppio della shell - questo non è indicato nel rapporto. Ma, a quanto pare, questo è successo all'interno della torre di comando, perché la forza dell'esplosione ha strappato le piastre dell'armatura del tetto e la piastra adiacente da 250 mm è stata semplicemente strappata dai supporti e dispiegata.

Quindi, con questo colpo, la penetrazione netta e il passaggio del proiettile dovrebbero essere contati per la protezione dell'armatura nel suo insieme.
Ma quando si è sparato # 9, si è verificato un piccolo incidente: il proiettile ha colpito l'armatura direttamente di fronte al pavimento da 70 mm. Di conseguenza, la piastra dell'armatura da 250 mm è stata perforata e anche il suo angolo, di circa 450x600 mm, si è rotto e nel pavimento da 70 mm è stata trovata una buca lunga 200 mm. Pertanto, si può affermare che anche in questo caso il proiettile non ha solo perforato l'armatura, ma lo ha fatto con una discreta quantità di energia, che è stata sufficiente per danneggiare un foglio di acciaio per armature da 70 mm posizionato orizzontalmente.
Di conseguenza, in quattro colpi su cinque, i proiettili perforanti russi hanno mostrato il risultato atteso, confermato dai calcoli secondo de Marr. Ma quando si è sparato n. 7, è successa una cosa strana: il proiettile ha colpito la piastra dell'armatura esattamente allo stesso modo, con lo stesso angolo di 80 ° e con la stessa velocità di 457 m / s, ma non ha perforato l'armatura, esplodendo durante il suo passaggio. Di conseguenza, si è rivelata una buca con una profondità di 225-250 mm: sono entrati solo "frammenti di un proiettile che pesava fino a 16 kg di peso".
Vediamo che su 4 colpi di proiettili perforanti da 305 mm, che avrebbero dovuto penetrare un'armatura di oltre 285 mm di spessore, solo 3 erano penetrazioni "pulite". In un caso, il proiettile è esploso mentre passava attraverso l'armatura, anche se dovrebbe non essere stato.
Qual è la ragione di questo fiasco? Forse è il guscio stesso? Supponiamo che un fusibile difettoso abbia funzionato prematuramente. Ma è possibile anche un'altra interpretazione: il fatto è che la penetrazione dell'armatura da parte di un proiettile è di natura probabilistica. Cioè, non esiste una cosa tale che, ad esempio, se, secondo la formula Jacob de Marr, lo spessore massimo dell'armatura perforata da un proiettile in determinate condizioni è di 285 mm, allora l'armatura di 286 mm non sarà penetrata dal proiettile in ogni caso. Potrebbe benissimo sfondare. E viceversa: rompi nelle stesse condizioni contro armature di spessore minore.
In altre parole, la stessa formula di Jacob de Marr (o qualsiasi altra analoga ad essa) non ha affatto accuratezza farmacologica. In realtà, ci sono intere gamme in cui un proiettile che colpisce una corazza ad un certo angolo e ad una certa velocità può penetrare l'armatura con un certo grado di probabilità, ma questo non può essere calcolato utilizzando formule di penetrazione dell'armatura generalmente accettate. E può darsi che nel caso del colpo n.7, la suddetta probabilità abbia funzionato.
Quindi, secondo me, i risultati dello scatto n. 7 sono casuali e non dovrebbero essere presi in considerazione. E l'armatura delle corazzate russe con uno spessore di 250 mm non poteva sopportare di essere colpita da 470,9 kg di un proiettile a una velocità di 457 m / se un angolo di incontro con un ostacolo di circa 80 °. Secondo de Marr, risulta che il coefficiente "K" dell'armatura russa in questo caso dovrebbe essere inferiore a 2228. Ma quanto?
La risposta a mio avviso si può ottenere analizzando le conseguenze del colpo n° 11. Il proiettile ha forato una lastra di 250 mm, ha colpito la parete opposta e vi ha fatto una buca di 100 mm. Quindi, possiamo supporre che la massima penetrazione dell'armatura del proiettile russo da 470,9 kg con i parametri sopra indicati fosse 250 mm dell'armatura cementata di Krupp. E altri 100 mm di armatura omogenea non cementata messi a parte.
Perché è omogeneo? Il fatto è che, come sai, l'armatura cementata consiste, per così dire, di due strati. Quello superiore è molto forte, ma allo stesso tempo fragile, e quindi inizia un'armatura più morbida, ma più viscosa. Il proiettile, colpendo la corazza da 250 mm, ha colpito lo strato "morbido e viscoso" dall'interno della timoneria, che nelle sue qualità è piuttosto simile all'armatura omogenea, piuttosto che cementata.
Inoltre, va tenuto presente che sto calcolando il coefficiente "K" per un proiettile che attraversa l'armatura nel suo insieme ed esplode dietro di essa. Ma nel caso del colpo n.11, questo non è quello che è successo: il proiettile, sfondando 250 mm dell'armatura cementata di Krupp e colpendo il lato posteriore della seconda piastra, non ha perforato l'armatura, ma è esplosa, e solo prendendo in conto dell'energia dell'esplosione, è riuscito a fare una buca di 100 mm. Pertanto, il calcolo di "250 mm cementato + 100 mm armatura omogenea" può considerarsi effettuato su ipotesi ovviamente sfavorevoli per l'armatura. Di conseguenza, il risultato ottenuto può essere considerato il minimo al di sotto del quale non avrà la resistenza dell'armatura Krupp di fabbricazione russa.
E poi il calcolo è molto semplice. La velocità del proiettile, come è stato detto molte volte sopra, è di 457 m / s, l'angolo di deviazione dalla normale quando colpisce la corazza da 250 mm è di 10°. Quando passa attraverso questa armatura, il proiettile "girerà" e colpirà la seconda piastra già con un angolo di 90 °, cioè una deviazione di 0 ° dalla normale. Questo segue dal diagramma n. 9 ““Corso di tattica navale. Artiglieria e Corazza "L. G. Goncharov, riportato a pagina 132. Dove, oltre alla forza dei proiettili all'impatto, c'è un grafico del giro del proiettile quando passa attraverso l'armatura, a seconda dell'angolo di incontro con questa armatura.
Il rapporto tra la resistenza dell'armatura dell'armatura russa omogenea e cementata mi è sconosciuto. Ma, secondo G. Evers, l'armatura cementata tedesca aveva un coefficiente "K" del 23% superiore a quello omogeneo. E, probabilmente, anche per l'armatura russa questo rapporto è vero. Inoltre, va tenuto presente che quando si passa attraverso una piastra di armatura da 250 mm, il proiettile perderà il suo cappuccio perforante. Ciò, al contrario, porterà ad un aumento dell'armatura omogenea "K" del 15%.
Quando si calcola la velocità di un proiettile per penetrare in una piastra omogenea da 100 mm, è stata utilizzata la stessa formula di una piastra cementata da 250 mm, è stato modificato solo il coefficiente "K". So che L. G. Goncharov ha raccomandato di utilizzare una formula diversa fornita nel suo libro di testo per l'armatura omogenea. Ma lei, secondo lui, è progettata per armature più sottili di 75 mm. Abbiamo, dopo tutto, 100 mm. Inoltre, secondo G. Evers, l'uso della suddetta formula di Jacob de Marr è applicabile anche per armature omogenee.
Secondo i risultati del calcolo della "K" dell'armatura russa cementata, ha un valore 2005. Ora vediamo se ci sono stati casi durante le riprese che hanno confutato questo risultato.
A proposito di sparare a un'armatura da 225 mm
Solo 2 colpi di proiettili perforanti sono stati sparati contro l'armatura da 225 mm. Inoltre, la velocità del proiettile al momento del contatto con l'armatura era di 557 m / s - una tale velocità avrebbe dovuto avere il proiettile a una distanza di 45 cavi. È vero, l'angolo di incontro con l'armatura era molto svantaggioso: una deviazione di 65 ° o 25 ° dalla normale. Ma anche in questo caso, per resistere all'impatto di 470, 9 kg del proiettile, la corazza dovrebbe avere un coefficiente "K" superiore a 2 690. Il che, ovviamente, è completamente impossibile. In altre parole, quando si sparava con tali parametri, anche l'armatura dell'era della seconda guerra mondiale doveva essere perforata con un'enorme quantità di energia dal proiettile.
E con il colpo n. 25, è esattamente quello che è successo. Il proiettile ha facilmente perforato la piastra dell'armatura da 225 mm (non ha nemmeno sfondato, ma ha semplicemente rotto un pezzo di 350x500 mm), quindi ha colpito lo smusso, che consisteva in un'armatura di 25 mm su un metallo da 12 mm substrato e ha praticato un foro 1x1, 3 su di esso M. La posizione esatta dello scoppio del proiettile non è stata stabilita. Ma si presumeva che fosse entrato nella sala macchine ed fosse già esploso lì. In altre parole, il risultato è stato esattamente quello che ci si aspetterebbe da un colpo del genere.
Ma con il secondo turno (scatto n. 27), tutto si è rivelato incomprensibile. Il proiettile ha deviato dal punto di mira. E, come dice il rapporto, "colpisci il bordo superiore dell'armatura". Il risultato dello scatto sarà più facile da citare dal documento:
“Il proiettile ha fatto una buca nell'armatura profonda circa 75 mm e larga circa 200 mm e, strappando con un quadrato il bordo sporgente della maglia, è esploso senza rallentare qui, sprigionando fumo nero. La casematta n. 2 non è stata danneggiata.
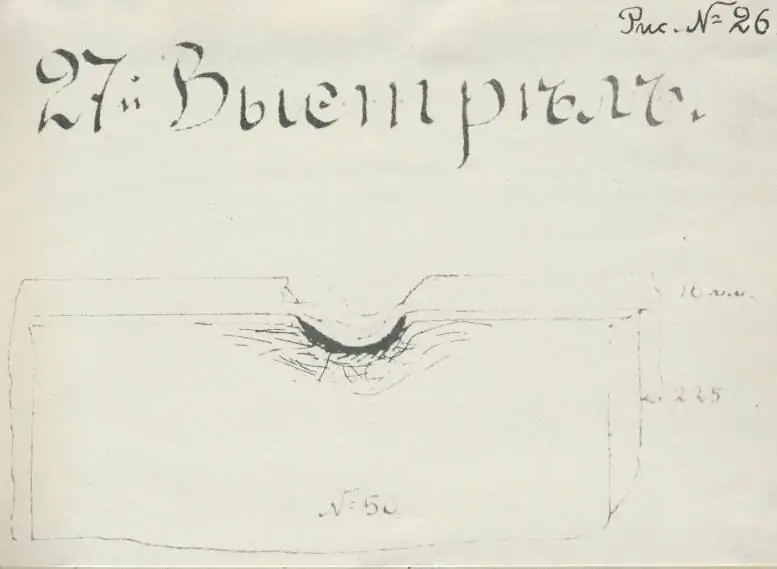
Non è del tutto chiaro cosa possa essere successo qui. Principalmente perché non è chiaro dove abbia colpito esattamente il proiettile. Per cominciare, "bordo" è esso stesso un concetto estensibile, poiché può essere usato, tra le altre cose, per significare "il bordo di qualcosa". Cioè, non è nemmeno chiaro se la linea centrale del proiettile abbia colpito la superficie verticale o orizzontale della corazza.
Ma in presenza di un fusibile di alta qualità, ci si aspetterebbe un danno molto maggiore da ognuna di queste opzioni. Se il proiettile ha colpito il piano verticale dell'armatura, dovrebbe essere collassato a tutta la sua profondità, non di 75 mm. Se l'impatto è caduto sulla parte orizzontale, perché, allora, l'angolo dell'incontro dell'ostacolo è di circa 65 ° registrato nel rapporto? Il proiettile non è caduto dal cielo sulla superficie orizzontale della lastra da 225 mm, è stato sparato con un angolo di 65° rispetto alla superficie verticale, il che significa che avrebbe dovuto essere di 25° rispetto all'orizzontale. In questo caso, puoi aspettarti un rimbalzo. Oppure (in caso di scoppio di un proiettile) danni al ponte corazzato orizzontale da 37,5 mm adiacente al bordo superiore della corazza da 225 mm. Ma niente di tutto questo è successo.
Secondo me, la colpa era un proiettile difettoso che è crollato all'impatto, motivo per cui l'esplosione non si è rivelata in piena forza. O, forse, una miccia difettosa che ha fatto esplodere "alto esplosivo" nel momento in cui il proiettile ha toccato l'armatura. È anche possibile che il proiettile non fosse difettoso, ma sia crollato perché l'angolo formato dalle due superfici della corazza svolgeva il ruolo di una sorta di "mannaia". Formalmente, il proiettile non è penetrato nelle piastre da 225 mm. Ma in connessione con l'estrema insolita delle conseguenze del colpo, a mio avviso, la ragione non dovrebbe essere ricercata nelle qualità elevatissime della corazza.
Di conseguenza, i risultati del bombardamento delle piastre corazzate da 225 mm della "nave esclusa n. 4" non confermano o confutano la nostra precedente conclusione.
Tuttavia, nel 1920 ci furono altri test storici su proiettili e armature domestiche. Qui l'obiettivo era completamente diverso. Il compartimento sperimentale è stato costruito sotto lo Zar-Padre per determinare lo schema di protezione ottimale per le future corazzate russe. Ma nel 1917 qualcosa andò storto con l'autocrazia in Russia. E i progetti per la costruzione di dreadnought sono passati nella categoria dei progetti. Tuttavia, sono stati effettuati test, incluso - utilizzando proiettili da 305 mm 470, 9 kg. I risultati sono molto interessanti. Ma di questo parleremo nel prossimo articolo.
Ma quello che vorrei notare separatamente è la presenza di un'evidente stranezza nei test. Il fatto è che hanno deliberatamente sopravvalutato le distanze del fuoco di artiglieria.
Quindi, ad esempio, per i colpi con armature da 225 mm con proiettili perforanti, è indicato che la distanza corrispondente ai parametri del proiettile è di 65 cavi. Ma questo non è vero: a una velocità di 557 m / s con una deviazione dalla normale di 25 °, un proiettile da 305 mm avrebbe dovuto penetrare nell'armatura di circa l'8% più spesso rispetto a quando si sparava a 65 cavi, dove la velocità del proiettile sarebbe sono stati 486,4 m, e la deflessione dal normale - 10, 91 °.
Certo, si può sospettare un banale errore nei calcoli dell'autore dell'articolo, cioè io. Ma come capire quindi lo sparo alla torre di comando - qui nei documenti la velocità del proiettile è indicata la stessa deviazione di 557 m / s dalla normale - solo 10 °, ma la distanza è considerata la stessa, cioè 65 cavi ! In altre parole, risulta che la "distanza appropriata" è stata indicata affatto senza tener conto dell'angolo di incidenza, solo in termini di velocità del proiettile?
Tuttavia, questa versione è facilmente verificabile. Secondo i miei calcoli, la velocità del proiettile per 60 cavi è 502,8 m / s e per 80 cavi è 444 m / s. Allo stesso tempo, i dati sul tiro a distanza di cannoni da 305 mm / 52 forniti da L. G. Goncharov ("Corso di tattica navale. Artiglieria e armatura", p. 35), mostra per queste distanze rispettivamente 1671 e 1481 piedi / s, cioè tradotti nel sistema metrico - 509 e 451 m / s.
Quindi, possiamo presumere che la mia calcolatrice dia ancora un certo errore verso il basso, pari a 6-7 m / s. Ma è ovvio che 557 m/s per 65 cavi e 457 m/s per 83 cavi sono fuori questione qui.
E un altro fatto che ti fa pensare. Come puoi vedere, un totale di 7 colpi di proiettili perforanti da 305 mm sono stati sparati contro un'armatura da 225-250 mm. Allo stesso tempo, le condizioni di tiro erano tali che l'armatura specificata doveva sfondare con un margine considerevole. Tuttavia, in condizioni reali di tiro, anche se a distanza, solo in cinque casi su sette proiettili hanno perforato l'armatura. E solo 4 proiettili sono passati all'interno.






