- Autore Matthew Elmers [email protected].
- Public 2024-01-11 08:05.
- Ultima modifica 2025-01-24 09:27.
In questo articolo cercheremo di comprendere la penetrazione dell'armatura dei cannoni delle corazzate Bayern, Rivenge e Pennsylvania, nonché la qualità comparativa delle armature tedesche, americane e britanniche. È estremamente difficile farlo, perché i dati sui cannoni americani da 356 mm, tedeschi da 380 mm e britannici da 381 mm sono molto approssimativi e incompleti e talvolta si contraddicono a vicenda, ma proveremo comunque.
Qual è esattamente il problema? Vediamo come la maggior parte degli appassionati di storia navale (e non solo) confronta la penetrazione dell'armatura di alcune armi. Ad esempio: in una pubblicazione dedicata, ad esempio, alle corazzate inglesi, ci sono informazioni secondo cui un proiettile britannico da 381 mm della prima guerra mondiale ha perforato la corazza da 381 mm a una distanza di circa 70 cavi. In un'altra edizione, dedicata alle già navi "capitali" tedesche - che un simile proiettile tedesco da 380 mm "padroneggiava" un'armatura da 350 mm con solo 67, 5 cavi. Da ciò sembra derivare che il cannone inglese sia più potente - questa è precisamente la conclusione tratta.
Tuttavia, in realtà, confrontare dati come questo in questo modo è molto facile da confondere.
I dati di cui sopra sono ottenuti come risultato di sparatorie effettive o sono calcolati utilizzando tecniche di penetrazione dell'armatura? Se questi sono i risultati dello sparo effettivo, le condizioni erano identiche per entrambe le pistole? Se la penetrazione dell'armatura è stata ottenuta mediante calcolo, sono stati utilizzati gli stessi metodi? I dati ottenuti sono il risultato del lavoro di specialisti dei ministeri e dei dipartimenti competenti o sono il risultato di calcoli di storici che hanno utilizzato una calcolatrice? È chiaro che nel secondo caso la precisione sarà molto inferiore… Non bisogna andare lontano per gli esempi: prendiamo la famosa monografia di S. Vinogradov, "Supercorazzate del Secondo Reich" Bayern "e" Baden ". Nell'Appendice n. 2, lo stimato storico, insieme a V. L. Kofman fa una grande quantità di calcoli per confrontare le capacità delle corazzate Rivenge e Bayern. Ma ahimè, basta guardare la tabella dei parametri per i cannoni da 15 pollici (p. 124) e vedremo che, secondo i calcoli di autorevoli autori, un cannone inglese da 381 mm con un angolo di elevazione di 20, 25 gradi ha una portata di soli 105 cavi, ovvero circa 19, 5 mila m. Mentre fonti estranee per la stessa velocità iniziale (732 m / s) e un angolo di elevazione leggermente inferiore (20 gradi) danno distanze significativamente maggiori - 21, 3-21, 7 mila m Naturalmente, tuttavia, tali deviazioni dai valori reali hanno l'effetto più negativo sui risultati del calcolo.
Ma anche se le fonti presentano i risultati di calcoli di specialisti, la cui accuratezza non c'è dubbio, sorge un altro fattore che complica il confronto: il punto qui è la qualità dell'armatura. È chiaro che gli stessi britannici, nel calcolare la penetrazione dell'armatura durante la progettazione di una particolare corazzata, usavano gli indicatori corrispondenti dell'armatura britannica, i tedeschi, rispettivamente, il tedesco, ecc. E l'armatura di diversi paesi può differire in termini di durata, ma questo è ancora metà del problema: dopotutto, in un singolo paese, la stessa armatura Krupp veniva costantemente migliorata. Pertanto, risulta che i calcoli dei sistemi di artiglieria, effettuati, ad esempio, in Inghilterra e apparentemente per la stessa armatura Krupp, ma realizzati in tempi diversi, potrebbero rivelarsi incomparabili. E se a questo aggiungiamo l'assenza quasi totale di lavori seri sull'evoluzione della cassa dell'armatura in vari paesi del mondo …
In generale, un confronto più o meno affidabile della penetrazione dell'armatura non è un compito così semplice come potrebbe sembrare a prima vista. E, in modo amichevole, un laico (che, senza dubbio, è l'autore di questo articolo) è meglio non affrontare questa questione. Ma, ahimè, con nostro profondo rammarico, i professionisti in qualche modo non hanno fretta di affrontare questi problemi, quindi … come si suol dire, in assenza di carta bollata, scriviamo in chiaro.
Certo, non è più possibile effettuare prove in scala reale dei suddetti sistemi di artiglieria, quindi il nostro destino sono i calcoli. E se è così, allora è necessario dire almeno un paio di parole sulle formule di penetrazione dell'armatura. Se vengono pubblicati metodi di calcolo moderni, di solito viene fornita la formula di Jacob de Marr solo in edizioni chiuse e nella letteratura popolare. È interessante che il Professore dell'Accademia Navale L. G. Goncharov, nel suo libro di artiglieria del 1932, la chiamò la formula di Jacob de Marr. Questa formula, insieme a molte altre, era diffusa all'inizio del secolo scorso e, devo dire, è abbastanza accurata - forse è anche la più accurata tra formule simili di quegli anni.
La sua particolarità sta nel fatto che non è fisico, cioè non è una descrizione matematica di processi fisici. La formula di De Marr è empirica, riflette i risultati del bombardamento sperimentale di armature di ferro e acciaio-ferro. Nonostante questa "natura non scientifica", la formula di de Marr ha mostrato una migliore approssimazione ai risultati effettivi delle riprese e sull'armatura Krupp rispetto ad altre formule comuni, e quindi la useremo per i calcoli.
Gli interessati troveranno questa formula nell'appendice di questo articolo, ma non è necessario costringere tutti coloro che leggono questo materiale a capirlo - questo non è necessario per comprendere le conclusioni dell'articolo. Notiamo solo che il calcolo utilizza concetti molto semplici e familiari a tutti coloro che sono interessati alla storia delle flotte militari. Questi sono la massa e il calibro del proiettile, lo spessore dell'armatura, l'angolo con cui il proiettile colpisce l'armatura, nonché la velocità del proiettile quando colpisce la corazza. Tuttavia, de Marr, ovviamente, non poteva limitarsi ai parametri di cui sopra. Dopotutto, la penetrazione di un proiettile dipende non solo dal suo calibro e dalla sua massa, ma anche, in una certa misura, dalla sua forma e dalla qualità dell'acciaio di cui è fatto. E lo spessore della corazza, che il proiettile è in grado di superare, dipende, ovviamente, non solo dalle prestazioni del proiettile, ma anche dalla qualità dell'armatura. Pertanto, de Marr ha introdotto un coefficiente speciale nella formula, che, di fatto, è progettato per tenere conto delle qualità indicate dell'armatura e del proiettile. Questo coefficiente aumenta con un aumento della qualità dell'armatura e diminuisce con un deterioramento della forma e della qualità del proiettile.
In effetti, la principale difficoltà nel confrontare i sistemi di artiglieria di diversi paesi è proprio "posa" proprio su questo coefficiente, che in futuro chiameremo semplicemente (K). Dovremo trovarlo per ciascuno degli strumenti di cui sopra, se, ovviamente, vogliamo ottenere un risultato in qualche modo corretto.
Quindi, prendiamo prima dei dati abbastanza diffusi sulla penetrazione dell'armatura del cannone tedesco da 380 mm / 45 "Bayern", secondo il quale il cannone a una distanza di 12.500 m (gli stessi cavi da 67, 5) potrebbe penetrare 350 mm di armatura. Usiamo un calcolatore balistico per trovare i parametri di un proiettile da 750 kg, con una velocità iniziale di 800 m / s al momento dell'impatto sull'armatura: si scopre che un tale proiettile colpirà una corazza posizionata rigorosamente verticalmente a un angolo di 10,39 gradi, con una velocità di 505,8 m/sec. Un piccolo disclaimer: di seguito, quando parliamo dell'angolo di impatto del proiettile, intendiamo il cosiddetto "angolo dal normale". "Normale" è quando il proiettile colpisce la bonneplite rigorosamente perpendicolare alla sua superficie, cioè con un angolo di 90 gradi. Di conseguenza, il proiettile ha colpito con un angolo di 10 gradi.dal normale significa che ha colpito la lastra con un angolo di 80 gradi. alla sua superficie, deviando dal "riferimento" di 90 gradi. di 10 gradi.
Ma torniamo alla penetrazione della corazza del cannone tedesco. Il coefficiente (K) in questo caso sarà approssimativamente (arrotondato all'intero più vicino) pari a 2.083 - questo valore dovrebbe essere considerato abbastanza normale per l'armatura dell'era della prima guerra mondiale. Ma qui sorge un problema: il fatto è che la fonte dei dati sulla penetrazione dell'armatura è il libro "Capitali tedesche della seconda guerra mondiale", in cui il cannone da 380 mm / 45 del Bayern è stato confrontato con il calibro principale della corazzata "Bismarck". E non potrebbe essere che il calcolo tenesse conto degli indicatori dell'armatura Krupp, creata nell'intervallo tra le due guerre mondiali, che era molto più forte di quella installata su Bayenne, Rivenge e Pennsylvania? Inoltre, l'enciclopedia elettronica navweaps riporta che ci sono prove che a una distanza di 20.000 m i proiettili tedeschi da 380 mm erano in grado di penetrare la corazza di 336 mm, e stiamo parlando di armature dell'era della prima guerra mondiale.
Bene, crediamo: a 20 km, l'angolo di incidenza sarà di 23,9 gradi, la velocità del proiettile sull'armatura è di 410,9 m / s e il coefficiente (K) - alcuni sfortunati 1618, che non si adattano all'armatura valori di resistenza a tutte le epoche della prima guerra mondiale. Un risultato simile generalmente avvicina l'armatura Krupp di fabbricazione tedesca alla resistenza dell'armatura omogenea … Ovviamente, i dati di navweaps contengono una sorta di errore.
Proviamo allora ad utilizzare un'altra fonte di informazioni. Finora abbiamo utilizzato i dati calcolati, e ora proveremo a confrontarli con i risultati di prove reali del cannone tedesco da 380 mm / 45: quelli sono riportati da S. Vinogradov nella citata monografia dedicata al tedesco corazzate.
Descrive le conseguenze di 3 colpi con proiettili perforanti, contro piastre di armatura con uno spessore di 200, 290 e 450 mm, quest'ultima è la più interessante per noi: un proiettile del peso di 734 kg ha colpito la piastra di armatura con un angolo di 0 (cioè a 90 gradi rispetto alla superficie) e ad una velocità di 551 m / s punzonato 450 mm attraverso la lastra. Un risultato simile corrisponde al coefficiente (K) 1 913, ma, in effetti, sarà leggermente inferiore, perché i tedeschi hanno trovato il loro proiettile ben 2530 m dietro l'ostacolo che ha perforato, e - in generale. Purtroppo, non avendo alcun dato su quanto di questa distanza il proiettile ha volato nell'aria, quanto - "cavalcato" a terra, è assolutamente impossibile determinare l'energia immagazzinata da esso dopo la penetrazione dell'armatura.
Prendiamo ora il sistema di artiglieria britannico 381 mm / 42. Purtroppo, i dati sulla penetrazione dell'armatura sono piuttosto vaghi: ad esempio, V. L. Kofman, c'è una menzione del fatto che queste pistole britanniche hanno perforato l'armatura, lo spessore del loro stesso calibro a una distanza di circa 70 cavi. Ma con quale proiettile e con quale velocità iniziale? Tenendo conto del fatto che il riferimento è contenuto nella monografia dedicata all'incrociatore da battaglia "Hood", e si riferisce al periodo della creazione di questa nave, si può presumere che si tratti di un guscio da 871 kg. Tuttavia, qui sorge un'altra domanda: la velocità iniziale ufficiale di un tale proiettile era di 752 m / s, ma alcuni calcoli dagli inglesi sono stati eseguiti a una velocità inferiore di 732 m / s, quindi quale valore dovremmo prendere? Tuttavia, qualunque sia la velocità indicata prendiamo, il coefficiente (K) oscillerà entro 1 983 - 2 048, e questo è più alto di quello che abbiamo calcolato per il valore (K) per il cannone tedesco. Si può presumere che questo parli della superiorità della qualità dell'armatura britannica rispetto a quella tedesca … o è che la forma geometrica del proiettile tedesco fosse più adatta per penetrare l'armatura? O forse il punto è che i dati di V. L. Kofman sono valori calcolati, ma in pratica i proiettili britannici otterrebbero un risultato migliore?
Bene, abbiamo a nostra disposizione dati sui risultati del bombardamento della corazzata "Baden"

Quindi, uno dei proiettili britannici, che colpisce con un angolo di 18 gradi. alla velocità di 472 m / sec., "sopraffatto" l'armatura frontale da 350 mm della torretta tedesca di grosso calibro. Questi dati sono tanto più preziosi perché in questo caso, l'armatura non britannica, ma tedesca è stata sottoposta a bombardamento, cioè i test dei cannoni da 381 mm / 42 e 380 mm / 45 sono, quindi, in un unico sistema di coordinate.
Ahimè, non ci aiutano molto. Se assumiamo che il proiettile inglese abbia perforato la torre tedesca, come si suol dire, "con l'ultimo pezzo di forza" e se ci fosse stata un'armatura da 351 mm, avrebbe fallito, allora il suo (K) sarebbe uguale a 2.021. è interessante, tra l'altro, che S. Vinogradov affermi che il proiettile britannico, che ha penetrato l'armatura frontale da 350 mm della torre tedesca, non è stato successivamente trovato, ma in realtà il rapporto afferma qualcos'altro: è esploso, e c'è un descrizione di dove i frammenti volarono nella torre.
Naturalmente, non abbiamo motivi assoluti per presumere che questa penetrazione fosse il limite per un proiettile da 381 mm, o addirittura vicino a quello. Tuttavia, secondo alcuni segni indiretti, si può presumere che fosse esattamente così. Un altro colpo "suggerisce" a questo: un proiettile britannico da 871 kg che colpisce una barbetta da 350 mm con un angolo di 11 gradi, sebbene sia stato in grado di fare un buco nell'armatura con un diametro di 40 cm, non è entrato nella barbetta stesso, esplodendo nel processo di superamento dell'armatura. In questo caso, il colpo è avvenuto quasi al centro del barbet, cioè la curvatura della corazza, se ha avuto qualche influenza, è stato il minimo.
Da tutto quanto sopra, si può provare a trarre alcune conclusioni, ma, a causa della fragilità della base di prove, esse, ovviamente, saranno di natura molto congetturale.
Conclusione 1: l'armatura tedesca durante la prima guerra mondiale corrispondeva grosso modo a quella britannica in termini di durata. Questa conclusione è valida se la dichiarazione di V. L. Kofman che il cannone britannico da 381 mm / 42 fosse in grado di penetrare armature pari al suo calibro di 70 kbt, e se non ci sbagliavamo nell'ipotesi che la penetrazione di 350 mm della piastra frontale della torretta tedesca ad un angolo di 18 gradi e una velocità di 472 m/s… è il limite o molto vicino al limite di penetrazione del proiettile britannico da 381 mm.
Conclusione 2°. Apparentemente, la forma e la qualità del proiettile tedesco da 380 mm gli hanno fornito una migliore penetrazione dell'armatura rispetto a quella inglese. Sulla base dei dati di cui sopra, possiamo supporre che il coefficiente (K) del proiettile britannico da 381 mm quando si spara contro l'armatura tedesca fosse di circa 2.000, mentre il proiettile tedesco da 380 mm era di circa 1.900. Se il nostro primo è corretto la conclusione che il la resistenza dell'armatura dell'armatura britannica e tedesca è approssimativamente equivalente, è ovvio che l'unica ragione per il coefficiente più basso (K) può essere solo il proiettile stesso.
Perché una granata tedesca potrebbe essere migliore? Il suo calibro è leggermente più piccolo, di un millimetro, ma, ovviamente, questo non potrebbe avere alcun effetto significativo. Il calcolo mostra che con la stessa massa (750 kg), un cambiamento di calibro di 1 millimetro porterà ad un aumento della penetrazione dell'armatura di 1,03 millimetri. Anche il proiettile tedesco è più corto: la sua lunghezza era di calibro 3,5, mentre la lunghezza del "Greenboy" britannico è di calibro 4. Potrebbero esserci state anche altre differenze. Naturalmente, la qualità dell'acciaio con cui è realizzato il proiettile gioca un ruolo significativo qui.
Ora calcoliamo la penetrazione dell'armatura dei cannoni tedeschi e britannici per una distanza di 75 cavi - una distanza generalmente accettata per una battaglia decisiva, dove ci si poteva aspettare abbastanza colpi per distruggere una nave nemica della linea.
Alla distanza indicata, 871 kg di un proiettile di cannone britannico da 381 mm / 42, sparato a una velocità iniziale di 752 m / s, ha colpito la corazza posizionata verticalmente con un angolo di 13,05 gradi e la sua velocità "sul piatto" era 479,6 m / s … Con (K) pari a 2.000, secondo la formula di Jacob de Marr, la penetrazione dell'armatura del proiettile britannico era di 376,2 mm.
Per quanto riguarda il guscio tedesco, tutto è un po' più complicato. Se la nostra conclusione che ha superato l'inglese in termini di penetrazione dell'armatura è corretta, le capacità del cannone tedesco da 380 mm / 45 su 75 cavi erano molto vicine al cannone inglese da quindici pollici. A questa distanza, il proiettile tedesco da 750 kg ha colpito il bersaglio con un angolo di 12,42 gradi a una velocità di 482,2 m / s e a (K) pari a 1.900, la penetrazione dell'armatura era di 368,9 mm. Ma se l'autore di questo articolo si sbaglia ancora e per la pistola tedesca vale la pena usare lo stesso coefficiente della pistola inglese, le capacità del proiettile da 380 mm scendono a 342,9 mm.
Tuttavia, secondo l'autore, la penetrazione dell'armatura del proiettile tedesco è più vicina a 368,9 mm (dopotutto, il tiro pratico ha prodotto un coefficiente di 1 913, nonostante il fatto che il proiettile abbia volato quindi 2,5 km), ma la penetrazione dell'armatura del proiettile inglese può essere leggermente inferiore calcolato. In generale, si può considerare che a una distanza di 75 cavi, i sistemi di artiglieria britannico e tedesco sono abbastanza comparabili in termini di penetrazione dell'armatura.
Ma con la pistola americana da 356 mm / 45, tutto si è rivelato molto più interessante. I dati precedentemente citati per conchiglie del peso di 680 kg dovrebbero essere considerati canonici nella letteratura in lingua russa.
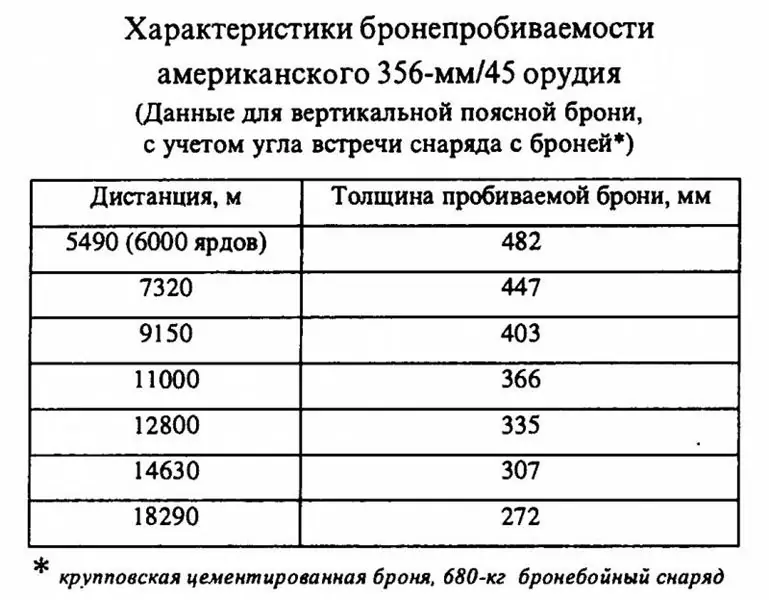
In effetti, i valori in essa indicati sembrano portare a conclusioni del tutto ovvie: se anche i proiettili da 680 kg apparsi negli Stati Uniti dopo il 1923 sono inferiori nella penetrazione della corazza ai loro europei da 380-381 mm " colleghi", allora cosa parla davvero dei precedenti proiettili da 635 kg, che erano dotati di artiglieria da 356 mm delle corazzate americane! Sono più leggeri, il che significa che perdono velocità più velocemente in volo, mentre la loro velocità iniziale non superava i proiettili più pesanti, e in termini di forma e qualità, le munizioni del 1923 dovrebbero avere un vantaggio. È chiaro come il giorno che la "Pennsylvania" americana al momento dell'entrata in servizio era inferiore in termini di penetrazione della corazza alle corazzate britanniche e tedesche. Beh, è ovvio, no?
Questa è esattamente la conclusione che l'autore ha fatto, considerando le capacità dei cannoni americani da quattordici pollici nell'articolo corazzate "Standard" degli Stati Uniti, della Germania e dell'Inghilterra. "Pennsylvania" americana ". E poi ha preso una calcolatrice …
Il fatto è che il calcolo secondo la formula de Marra ha mostrato che i cannoni americani 356-mm / 45 avevano la penetrazione dell'armatura indicata nella tabella con un coefficiente (K) pari a 2.317! In altre parole, i proiettili americani da 680 kg mostrati nella tabella hanno mostrato i risultati quando esposti a armature che non sono state create nell'era della prima guerra mondiale, ma su campioni molto più tardi e più durevoli.
È difficile dire quanto sia aumentata la forza della protezione dell'armatura nell'intervallo tra la prima e la seconda guerra mondiale. Nelle fonti in lingua russa, ci sono solo brevi e spesso contraddittori riferimenti a questo problema, in base ai quali si può presumere che la forza dell'armatura di Krupp sia aumentata di circa il 20-25%. Pertanto, per i proiettili di grosso calibro dell'era del Primo Mondo, la crescita del coefficiente (K) sarà da 1.900 - 2.000 a 2.280 - 2.500, ma qui va ricordato che con un aumento della qualità della protezione dell'armatura, ovviamente, anche la qualità dei proiettili è aumentata, e quindi per le munizioni pesanti della seconda guerra mondiale (K) potrebbe essere inferiore. Pertanto, (K) nella quantità di 2.317 per i proiettili del dopoguerra, naturalmente migliorati tenendo conto dell'esperienza acquisita in precedenza, sembra abbastanza organico, ma per l'armatura dell'era della seconda guerra mondiale, non la prima.
Ma impostando il coefficiente (K) per i proiettili americani da 680 kg al livello di 2.000, cioè portando la qualità della protezione dell'armatura all'era della prima guerra mondiale, per una distanza di 75 cavi otterremo l'armatura penetrazione a livello di 393,5 mm, cioè superiore a quella dei cannoni da quindici pollici britannici e tedeschi!

La conversione in un proiettile da 635 kg fornisce una correzione molto insignificante - il calcolatore balistico ha mostrato che a una distanza di 75 cavi, con un angolo di incidenza di 10, 82 gradi. e la velocità "sull'armatura" 533, 2 m a (K) pari a 2.000, il proiettile americano penetra nell'armatura dell'era della prima guerra mondiale, spessa 380 mm, cioè molto più del suo stesso calibro!
D'altra parte, è del tutto possibile che un tale calcolo non sia ancora del tutto corretto. Il fatto è che, secondo alcuni rapporti, il coefficiente (K) per la stessa armatura diminuisce all'aumentare del calibro del proiettile. Quindi, ad esempio, nei nostri calcoli, il valore massimo (K) per il sistema di artiglieria tedesco 380-mm / 45, ottenuto mediante calcolo e pubblicato nelle fonti, è 2.083. Allo stesso tempo, i calcoli per il tedesco 305-mm / 50 cannoni, che sono stati installati sulle navi Kaiserlichmarine a partire da Helgolands, i dati provenienti da fonti sulla penetrazione dell'armatura danno (K) al livello di 2.145. Di conseguenza, è possibile che i cannoni da 356 mm / 45 (K) = 2.000 abbiamo preso per calcolare la penetrazione della corazza dei cannoni americani è ancora troppo piccola.
Inoltre, sfortunatamente, l'autore non ha "indizi" per confrontare la resistenza dell'armatura dell'armatura Krupp americana con le sue controparti europee. Non resta altro che considerarlo equivalente alla protezione dell'armatura tedesca e inglese, anche se questo, ovviamente, potrebbe non essere il caso.
Riassumiamo tutti questi dati piuttosto caotici. Tenendo conto degli errori dei "metodi" utilizzati nei calcoli, si può ipotizzare con un alto grado di probabilità che La penetrazione dell'armatura della protezione dell'armatura verticale dei cannoni di calibro principale delle corazzate Rivenge, Bayern e Pennsylvania a una distanza di 75 cavi era approssimativamente la stessa ed era di circa 365-380 mm.
Nonostante una serie di ipotesi, i dati a nostra disposizione ci consentono comunque di trarre alcune conclusioni sulla protezione dell'armatura verticale. Ma con lo sfondamento delle barriere orizzontali, che sono ponti corazzati, tutto è molto più complicato. Il fatto è che Jacob de Marr, sfortunatamente, non si è affatto preoccupato di creare una formula per determinare la forza della difesa orizzontale. La sua formula di base, adattata ai moderni tipi di armatura, è adatta solo per il calcolo di armature cementate con uno spessore superiore a 75 mm. Questa formula è fornita nell'appendice n. 1 di questo articolo e tutti i calcoli precedenti nell'articolo sono stati effettuati utilizzandola.
Ma i ponti delle navi di quegli anni erano protetti non da un'armatura cementata (eterogenea) ma da un'armatura omogenea, che mancava di uno strato superficiale indurito. Per tale armatura (ma - installata verticalmente!), Viene utilizzata una formula diversa, destinata alla valutazione di armature non cementate con uno spessore inferiore a 75 mm, è riportata nell'appendice n. 2.
Tengo a precisare che entrambe queste formule sono tratte da una fonte più che seria: “Il corso della tattica navale. Artiglieria e armature 1932, autore - Professore dell'Accademia Navale RKKA L. G. Goncharov, uno dei massimi esperti dell'URSS prebellica nel campo dell'artiglieria navale.
E ahimè, nessuno di questi è adatto per valutare la durata della protezione orizzontale. Se usiamo la formula per l'armatura cementata, a una distanza di 75 cavi otteniamo una scarsa penetrazione dell'armatura: 46,6 mm per 381 mm / 42 britannici, 39,5 mm per 380 mm / 45 tedeschi e 33,8 mm per 356 mm / 45 americani pistole. Se usiamo la seconda formula per l'armatura non cementata, otteniamo che quando colpiti con un angolo tipico per una distanza di 75 cavi, tutti e tre i sistemi di artiglieria penetrano facilmente nella piastra dell'armatura da 74 mm, dopo di che mantengono un'enorme quantità di energia cinetica - ad esempio, l'inglese 381- mm, un proiettile per penetrare armature di questo spessore a una distanza di 75 cavi avrà una velocità di 264,5 m/s, mentre la sua velocità sarà di 482,2 m/s. Se ignoriamo la limitazione dello spessore della piastra di armatura, si scopre che il proiettile britannico da 381 mm, secondo la formula sopra, è in grado di penetrare nell'armatura del ponte con uno spessore di oltre 180 mm! Il che, ovviamente, è del tutto impossibile.
Se proviamo a fare riferimento ai risultati dei test della corazzata di classe Bayern, vedremo che i proiettili britannici da 871 kg perforanti hanno colpito due volte l'armatura orizzontale delle torri, che aveva uno spessore di 100 mm con un angolo di 11 gradi, che corrisponde a una distanza di 67,5 cavi per un proiettile con una velocità iniziale di 752 m / se 65 cavi - per un proiettile con una velocità iniziale di 732 m / s. Entrambe le volte l'armatura non è stata forata. Ma in un caso, il proiettile, rimbalzando, ha fatto un solco nell'armatura con una profondità di 70 cm, cioè la piastra era piegata molto fortemente. E nel secondo, sebbene il guscio, di nuovo, rimbalzasse, l'armatura non era solo concava di 10 cm, ma anche strappata.

La natura simile del danno suggerisce che, sebbene l'armatura tedesca da 100 mm fornisse protezione alle distanze indicate, era, se non al limite del possibile, molto vicina a quella. Ma il calcolo secondo la formula per l'armatura cementata fornisce una penetrazione dell'armatura di soli 46,6 mm a una distanza maggiore, dove l'angolo di incidenza sarà maggiore e, di conseguenza, sarebbe più facile per il proiettile penetrare nell'armatura del ponte. Cioè, secondo la formula, si scopre che il ponte da 100 mm dovrebbe avere scherzosamente e con un ampio margine di sicurezza riflettere i proiettili inglesi - tuttavia, la pratica non lo conferma. Allo stesso tempo, secondo i calcoli che utilizzano la formula per l'armatura non cementata, risulta che i tetti del calibro principale del Baden avrebbero dovuto essere facilmente perforati e - con una grande quantità di energia del proiettile - che, ancora una volta, non è affatto confermato dalla pratica.
Devo dire che tali imprecisioni nei calcoli hanno una spiegazione completamente logica. Come abbiamo detto prima, le formule di de Marr non sono una descrizione matematica dei processi fisici, ma sono solo una fissazione dei modelli ottenuti durante il test dell'armatura. Ma è stata testata la protezione dell'armatura verticale, non orizzontale, e non sorprende affatto che i modelli in questo caso smettano semplicemente di funzionare: per l'armatura posizionata orizzontalmente, in cui i proiettili colpiscono con un angolo molto piccolo rispetto alla loro superficie, questi modelli, ovviamente sono completamente diversi.
L'autore di questo articolo ha trovato opinioni "su Internet" secondo cui le formule di de Marr funzionano efficacemente con angoli di deviazione dalla normale non più di 60 gradi, cioè da 30 gradi alla superficie della lastra e oltre. Si può presumere che questa valutazione sia molto vicina alla verità.
Pertanto, dobbiamo affermare con rammarico che l'apparato matematico a disposizione dell'autore non consente di eseguire calcoli affidabili della resistenza di protezione orizzontale delle corazzate Rivenge, Bayern e Pennsylvania. In considerazione di quanto sopra, sarà difficile utilizzare i dati sulla penetrazione dell'armatura dell'armatura orizzontale forniti in varie fonti - di norma, sono tutti basati sugli stessi calcoli secondo le formule di de Marr e non sono corretti.






